Physically-based BRDF
Contents
Introduction
Physically based rendering have been known for many years, but the "ad-hoc" rendering models (such as Phong) are still widely used in game. These "ad-hoc" models require laborious tweaking to produce high-quality images. However, physically based, energy-conserving rendering models easily create materials that hold up under a variety of lighting environments.
Surprisingly, physically based models are not more difficult to implement or evaluate than the traditional "ad-hoc" ones.
Since KlayGE 3.11.0, there is a calc_brdf() function in Lighting.fxml. It can be used for calculating the physically-based BRDF described by this article.
Reflectance equation
The most common used rendering model in game describes only reflectance, not including terms such as SSS. The reflectance equation is:
Here ρ(l, v) is BRDF, Li(l) is the contribution from light source, (n·l) is the angle between light and surface normal. This integration results the sum of all light sources contribute to a surface point.
Diffuse term
The simplest BRDF is the Lambert. The well-known Lambertian BRDF in game is present as (n·l). However, it is part of reflectance equation, and lambertian term is actually a constant value:
Punctual Light Sources
These are classic point, directional, and spot lights in compute games. These local light source can be abstracted to a concept named "punctual light sources". They are infinitely small light with centain direction. Since what we want is the lighting reach a surface point, we don't need to consider the attenuation. A punctual light source are parameterized by the light color clight and the light direction vector lc. The light color clight is specified as the color a white Lambertian surface would have when illuminated by the light from a direction parallel to the surface normal (lc = n).
How to calculate the contribution from this light source to a point? Here we will start by defining a tiny area light source centered on lc, with a small angular extent ε. This tiny area light illuminates a shaded surface point with the incoming radiance function Ltiny(l). The incoming radiance function has the following two properties:
The first property says that no light is incoming for any light directions which form an angle greater than ε with lc. The second property follows from the definition of clight. Since the surface is white, cdiff = 1. Applying reflectance equation and Lambert from last article, there's the second property. Because clight requires lc = n, it is the limit as ε goes to 0:
Since lc = n and ε→0, we can assume (n·l) = 1, which gives us:
That is:
Now we shall apply our tiny area light to a general BRDF, and look at its behavior in the limit as goes to 0:
So
As you see, the tiny area light source term disappears. The remaining of our equation is what we familar with.
Microfacet BRDF
The basis for most physically-based specular BRDF terms is microfacet theory. This theory was developed to describe surface reflection from general (non-optically flat) surfaces. The basic assumption underlying microfacet theory is that the surface is composed of many microfacets, too small to be seen individually. Each microfacet is assumed to be optically flat.
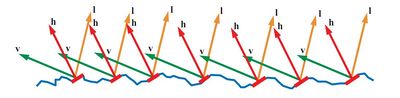
Each of these microfacets reflects light from a given incoming direction into a single outgoing direction which depends on the orientation of the microfacet normal m. When evaluating a BRDF term, both the light direction l and the view direction v are specified. This means that of all the millions of microfacets on the surface, only those that happen to be angled just right to reflect l into v have any contribution to the BRDF value. In the figure below, we can see that these active microfacets have their surface normal m oriented exactly halfway between l and v. We will denote it as h.
Not all microfacets for which m = h will contribute to the reflection; some are blocked by other microfacets from the direction of l (shadowing), from the direction of v (masking), or from both. Microfacet theory assumes that all shadowed light is lost from the specular term. The microfacet specular BRDF term has the following form:
F(l, h) is the Fresnel reflectance of the active microfacets (m = h). G(l, v, h) is the proportion of active microfacets which are not shadowed or masked. D(h) is the microfacet normal distribution function evaluated at the active microfacet normal m = h; in other words, the concentration of microfacets with normals equal to h. Finally, the denominator 4(n·l)(n·v) is a correction factor which accounts for quantities being transformed between the local space of the microfacets and that of the overall macrosurface.
Fresnel Term
The Fresnel reflectance term computes the fraction of light reflected from an optically flat surface. Its value depends on two things: the incoming angle (angle between light vector and surface normal) and the refractive index of the material. The Schlick approximation of Fresnel term is:
which cspec is the specular color.
Normal Distribution Term
In most surfaces, the microfacet's orientations are not uniformly distributed. Microfacet normals closer to the macroscopic surface normal tend to appear with smoother. The exact distribution is defined via the microfacet normal distribution function D(m). The function D() determines the size, brightness, and shape of the specular highlight. Normal distribution functions have some kind of "roughness" or variance parameter (anisotropic functions typically have two variance parameters).
Shadowing-Masking Term
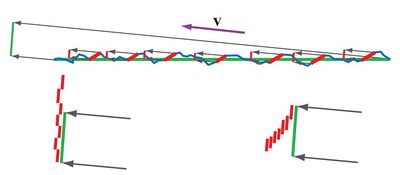
The shadowing and masking term G(l, v, h) is also often called the geometry term. In many cases, the shadowing-masking term partially cancels out the (n·l)(n·v) denominator in microfacet BRDF equation, replacing it with some other expression such as max(n·l, n·v). The shadowing-masking term is essential for BRDF energy conservation--without such a term the BRDF can reflect arbitrarily more light energy than it receives. A key part of the microfacet BRDF is the ratio between the active area (combined area of the microfacets which reflect light energy from l to v) and the total area (of the macroscopic surface). If shadowing and masking are not accounted for, then the active area may exceed the total area, an obvious impossibility which can lead to the BRDF not conserving energy, in some cases by a huge amount, as you see below:
On the top the flat macroscopic surface is shown in green, and the rugged microscopic surface is shown in blue. The facets for which m = h are marked in red. The projection of the macroscopic surface area onto the view direction is shown as a green line on the upper left. The projected areas of the individual red microfacets are shown as separate red lines. On the bottom left the areas of the red microfacets are added up without accounting for masking, resulting in an active area greater than the total area. So the BRDF illogically reflects more energy than it receives. On the right we see that the red areas are combined in a way that accounts for masking. The overlapping areas are no longer counted multiple times, and we see that the correct active area is smaller than the total area.
Comparison
The reflectance equation common used in game look like this:
According to Lambert equation, (n·lc) is part of reflectance equation, not diffuse term. So it should be:
where rv is the view vector reflected about the normal. It's from Phong model. It doesn't seem to correspond to anything from microfacet theory before. The Blinn-Phong model is very similar to this equation, but it uses the more physically meaningful half-vector h, which is microfacet's normal m. Changing from Phong to Blinn-Phong gives us the following model:
Recall the Lambert term, the diffuse term now is the same with physically-based one:
So, now we focus on specular term. If we look at the specular term only in the equation before:
Compare to microfacet specular:
Firstly, we can see from these two equations, the cspec in game can be replaced by Fresnel's F(cspec, lc, h).
Secondly, I mentioned before that D(h) is related to roughness. So D(h) and Blinn-Phong's (n·h)α have similar functions. However, to convert the (n·h)α term into a microfacet normal distribution function it must be correctly normalized. It means the sum of the signed projected areas of the microfacets needs to equal the signed projected area of the macroscopic surface; this must hold true for any viewing direction. Mathematically, this means that the function must fulfil this equation for any v:
This equation holds for any viewing direction. In the special case, v = n:
The Blinn-Phong cosine power term can be made to obey this equation by multiplying it with a simple normalization factor:
The only term left is:
It's shadowing/masking, or geometry term divided by the foreshortening factors. The physical meaning of this term is visibility. Since our modified specular model has no visibility term, we will simply set it to 1. That is:
This is actually a plausible geometry term for a heightfield microsurface (which is what the Blinn-Phong normal distribution function corresponds to, since it is zero for all backfacing microfacets). Gimplicit() is equal to 1 when l = n and v = n, which is correct for a heightfield (no microfacets are occluded from the direction of the macrosurface normal). It goes to 0 for either glancing view angles or glancing light angles, which again is correct (the probability of a microfacet being occluded by other microfacets increases with viewing angle).
Until now, several terms from microfacet specular BRDF are all explained, leaving us this rendering model:
The factor is because of ((α + 2) / 2π) * (π / 4) = (α + 2) / 8.
Add the diffuse term back, that is:
This is the final equation, which is physically-based rendering model, derivated by this serial. Compare to the model common used in game, the calculated amount increases little. However, this equation not only ensure the energy-preserving, but also easier for artists to adjust parameters.
Future works
A unsolved problem occurs in the context of very smooth surfaces with high specular powers. Such materials are important to model e.g., wet surfaces. However, the punctual light approximation breaks down in this case, yielding extremely intense highlights of subpixel size that are unrealistic and alias badly. What we would like to see is a sharp reflection of the shape of the light source, which requires some kind of area light approximation which is fast enough to use in games.
Another problem is that there are a variety of geometry terms in the literature. Do any of them provide a visual improvement over the "cheaper-than-free" implicit geometry function Gimplicit that is worth the extra cost? One candidate is the geometry factor proposed by Kelemen et. al. This is an approximation to the Cook-Torrance geometry factor but it is far cheaper to compute:
note that (lc·h) also exists in any case for Fresnel. It's a close approximation to the full Cook-Torrance geometry factor divided by the foreshortening terms.
The third problem is the Fresnel of diffuse term. It should be noted that there is no such thing as "a surface without specular". In reality such materials have cspec values around 0.03-0.06, and very low values of α (around 0.1-2.0). At glancing angles, even the most "matte" surfaces have noticeable specular appearance; the lack of this effect is another reason why so many game environments appear unrealistic.