Microfacet BRDF
大多数基于物理的specular BRDF的基础是microfacet理论。这个理论是用来描述来自于一般表面(不是光学平滑的)的反射。Microfacet理论的基本假设是,表面是由很多微平面(microfacet)组成,这些微平面都太小了,没有办法一个一个地看到;并假设每个microfacet都是光学平滑的。
每个microfacet把一个入射方向的光反射到单独的一个出射方向,这取决于microfacet的法向m。当计算BRDF的时候,光源方向l和视线方向v都得给定。这意味着在表面上的所有microfacet中,只有刚好把l反射到v的那部分对BRDF有贡献。在下图中,我们可以看到这些有效microfacet的表面法向m正好在l和v的中间,也就是h。
The basis for most physically-based specular BRDF terms is microfacet theory. This theory was developed to describe surface reflection from general (non-optically flat) surfaces. The basic assumption underlying microfacet theory is that the surface is composed of many microfacets, too small to be seen individually. Each microfacet is assumed to be optically flat.
Each of these microfacets reflects light from a given incoming direction into a single outgoing direction which depends on the orientation of the microfacet normal m. When evaluating a BRDF term, both the light direction l and the view direction v are specified. This means that of all the millions of microfacets on the surface, only those that happen to be angled just right to reflect l into v have any contribution to the BRDF value. In the figure below, we can see that these active microfacets have their surface normal m oriented exactly halfway between l and v. We will denote it as h.
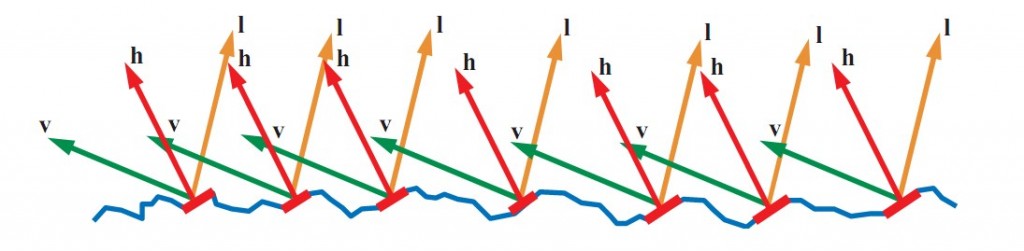
并不是所有m = h的microfacet对反射都有贡献。有些microfacet会在光源方向l被其他microfacet阻挡(shadowing),有些会在视线方向v被阻挡(masking),也可能都有。Microfacet理论假设所有被遮挡的没有对BRDF的贡献。Microfacet的specular BRDF可以表达成:
Not all microfacets for which m = h will contribute to the reflection; some are blocked by other microfacets from the direction of l (shadowing), from the direction of v (masking), or from both. Microfacet theory assumes that all shadowed light is lost from the specular term. The microfacet specular BRDF term has the following form:
$\rho(\mathbf{l}, \mathbf{v})=\frac{F(\mathbf{l},\mathbf{h})G(\mathbf{l},\mathbf{v},\mathbf{h})D(\mathbf{h})}{4(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})}$
$F(\mathbf{l}, \mathbf{h})$是有效microfacet(m = h)产生的Fresnel反射。$G(\mathbf{l}, \mathbf{v}, \mathbf{h})$是有效microfacet中没有被shadow或mask的比例。$D(\mathbf{h})$是microfacet的法线分布函数,或者说,microfacet的法线等于h的密度。最后,分母$4(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})$是个校正因子,用来校正从microfacet的局部空间转到整体表面的数量差异。
$F(\mathbf{l}, \mathbf{h})$ is the Fresnel reflectance of the active microfacets (m = h). $G(\mathbf{l}, \mathbf{v}, \mathbf{h})$ is the proportion of active microfacets which are not shadowed or masked. $D(\mathbf{h})$ is the microfacet normal distribution function evaluated at the active microfacet normal m = h; in other words, the concentration of microfacets with normals equal to h. Finally, the denominator $4(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})$ is a correction factor which accounts for quantities being transformed between the local space of the microfacets and that of the overall macrosurface.
Fresnel项
Fresnel反射项计算从光学平滑的表面反射的比率。它的值取决于两件事情:入射角(光源方向和表面法线之间的角),以及材质的折射率。Schlick近似的Fresnel项是:
Fresnel Term
The Fresnel reflectance term computes the fraction of light reflected from an optically flat surface. Its value depends on two things: the incoming angle (angle between light vector and surface normal) and the refractive index of the material. The Schlick approximation of Fresnel term is:
$F_{Schlick}(\mathbf{c}_{spec}, \mathbf{l}, \mathbf{h})=\mathbf{c}_{spec}+(1-\mathbf{c}_{spec})(1-\mathbf{l} \cdot \mathbf{h})^5$
其中$\mathbf{c}_{spec}$是specular颜色。
which $\mathbf{c}_{spec}$ is the specular color.
法线分布项
在大部分表面上,microfacet的方向不是均匀分布的。Microfacet的法线越接近宏表面的法线,就越光滑。这个分布由microfacet的法线分布函数D(m)来定义。函数D()决定了specular高光的大小、亮度和形状。 法线分布函数一般有类似于“粗糙度”这样的参数(各向异性的函数通常有两个参数)。
遮挡项(shadowing-masking term)
遮挡项G(l, v, h)也经常称为几何项 。在很多情况下,遮挡项在某种程度上抵消了microfacet方程中的$(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})$分母,替换成类似于$max(\mathbf{n} \cdot \mathbf{l}, \mathbf{n} \cdot \mathbf{v})$这样的形式。遮挡项对BRDF保能量是很重要的——没有这个项的话,BRDF反射出的能量可能比接收到的更多。Microfacet BRDF中很重要的一个事情是把能量从l反射到v的microfacet面积之和(有效面积)和宏表面总面积之间的比例。如果不考虑遮挡,那么有效面积可能会超过总面积,这回造成BRDF不保能量,甚至可能会很明显,如下图所示:
Normal Distribution Term
In most surfaces, the microfacet’s orientations are not uniformly distributed. Microfacet normals closer to the macroscopic surface normal tend to appear with smoother. The exact distribution is defined via the microfacet normal distribution function D(m). The function D() determines the size, brightness, and shape of the specular highlight. Normal distribution functions have some kind of “roughness” or variance parameter (anisotropic functions typically have two variance parameters).
Shadowing-Masking Term
The shadowing and masking term G(l, v, h) is also often called the geometry term. In many cases, the shadowing-masking term partially cancels out the $(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})$ denominator in microfacet BRDF equation, replacing it with some other expression such as $max(\mathbf{n} \cdot \mathbf{l}, \mathbf{n} \cdot \mathbf{v})$. The shadowing-masking term is essential for BRDF energy conservation–without such a term the BRDF can reflect arbitrarily more light energy than it receives. A key part of the microfacet BRDF is the ratio between the active area (combined area of the microfacets which reflect light energy from l to v) and the total area (of the macroscopic surface). If shadowing and masking are not accounted for, then the active area may exceed the total area, an obvious impossibility which can lead to the BRDF not conserving energy, in some cases by a huge amount, as you see below:
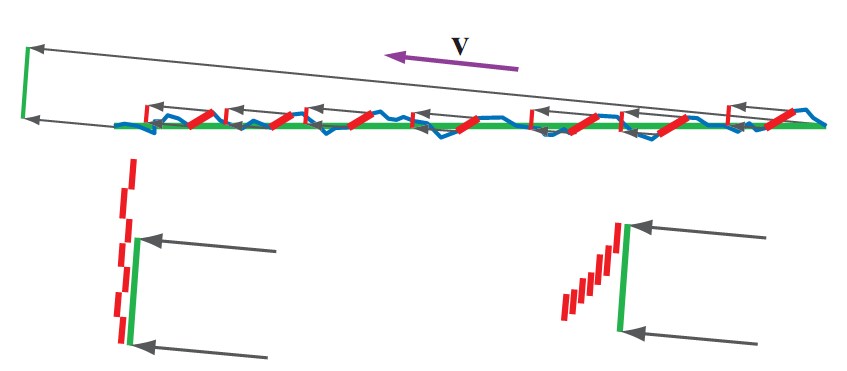
在上半部分,平的宏表面为绿色,粗糙的微观表面为蓝色。m = h的microfacet标记为红色。宏表面投到视线方向就是左上角的绿线。同时,投出来的单个红色的microfacet显示成独立的红线。左下图表示在没有遮挡项的情况下,红色的microfacet加起来的面积,结果就是有效面积大于总面积,所以BRDF的反射能量错误地大于了接收能量。右下图里红色区域考虑了遮挡,重叠的区域不再计算多次,所以有效面积小于总面积。
讲了这么多BRDF,本篇到此为止。下一篇将要揭示目前大多数游戏中所用的BRDF和基于物理的BRDF之间的区别。
On the top the flat macroscopic surface is shown in green, and the rugged microscopic surface is shown in blue. The facets for which m = h are marked in red. The projection of the macroscopic surface area onto the view direction is shown as a green line on the upper left. The projected areas of the individual red microfacets are shown as separate red lines. On the bottom left the areas of the red microfacets are added up without accounting for masking, resulting in an active area greater than the total area. So the BRDF illogically reflects more energy than it receives. On the right we see that the red areas are combined in a way that accounts for masking. The overlapping areas are no longer counted multiple times, and we see that the correct active area is smaller than the total area.
Talking so much about BRDF, this article ends here. The next article will explain the difference between BRDF in most current game and physically-based BRDF.





Comments