本系列源自于对Real Shading in Unreal Engine 4和Getting More Physical in Call of Duty: Black Ops II的理解。打算按照以前游戏中基于物理的渲染的思路,介绍一下如何在游戏这样的实时应用中使用基于物理的环境光。
回顾
在游戏中基于物理的渲染中列出了渲染方程的简化版,这是整个基于物理的体系的源头。
$L_0(\mathbf{v})=\int_{\Omega} \rho(\mathbf{l},\mathbf{v}) \otimes {L}_{i}(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
其中,根据microfacet理论,BRDF可以表达成:
$\rho(\mathbf{l}, \mathbf{v})=\frac{F(\mathbf{l},\mathbf{h})G(\mathbf{l},\mathbf{v},\mathbf{h})D(\mathbf{h})}{4(\mathbf{n} \cdot \mathbf{l})(\mathbf{n} \cdot \mathbf{v})}$
如之前的系列所述,这个公式只适合点光源。如果需要用到环境光,也就用cubemap光源做image based lighting(IBL),就需要推一个基于物理的环境BRDF。
Ground truth
仍然从渲染方程的简化版出发。因为不管是实时还是离线,要在的渲染中完成那个积分(即便是离散化)都是不实际的。一般来说需要用importance sampling减少计算量,也就是。
$L_0(\mathbf{v})=\int_{\Omega} \rho(\mathbf{l},\mathbf{v}) \otimes {L}_{i}(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
$\approx \frac{1}{N}\sum_{k=1}^N\frac{L_i(\mathbf{l_k})\rho(\mathbf{l_k}, \mathbf{v})(\mathbf{n} \cdot \mathbf{l_k})}{pdf(\mathbf{l_k}, \mathbf{v})}$
其中pdf是概率密度函数,根据Physically-Based Shading at Disney,
$pdf(\mathbf{l_k}, \mathbf{v})=\frac{D(\mathbf{h})(\mathbf{h} \cdot \mathbf{n})}{4(\mathbf{l} \cdot \mathbf{h})}$
用这个方程来计算specular的话,可以得到这样的结果:
上图的每个pixel都根据BRDF做了importance sampling,N=1024,BRDF是GGX,cubemap分辨率是512。在NVS 4200M上,只有2FPS的速度,即便在GTX 680上也只有30FPS。
传统做法
以前对于环境光,常见的做法就是prefilter。用AMD的cubemapgen对cubemap做一个prefilter,把卷积过的值存到mipmap的下几层。在渲染的时候,用roughness选择mipmap层次,根据反射方向采一个点,当作个方向光源来计算shading。Prefilter相当于对光源积分,所以这么做相当于把渲染方程组织成这样:
$L_0(\mathbf{v})=\rho(\mathbf{l},\mathbf{v}) (\mathbf{n} \cdot \mathbf{l})\otimes \int_{\Omega} {L}_{i}(\mathbf{l}) d \omega_{i}$
用这样的方式虽然能得到一个看起来不错的结果,但和ground truth比较的话,差别还是较大的。
接下去我会开始推导一个基于物理的环境BRDF。结果你会发现,基于物理的方法效果优于传统做法,并且开销更低了。
基于物理的做法
如果改变拆分的方式,把原方程近似成两个积分的乘积,就得到
$L_0(\mathbf{v}) \approx \int_{\Omega} {L}_{i}(\mathbf{l})d \omega_{i} \int_{\Omega} \rho(\mathbf{l},\mathbf{v}) (\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
其中,第一个积分仍是prefiltered cubemap。第二个积分还需要进一步推导。BRDF中的fresnel项是
$F_{Schlick}(\mathbf{c}_{spec}, \mathbf{l}, \mathbf{h})=\mathbf{c}_{spec}+(1-\mathbf{c}_{spec})(1-\mathbf{l} \cdot \mathbf{h})^5$
$= \mathbf{c}_{spec}(1-(1-\mathbf{l} \cdot \mathbf{h})^5)+(1-\mathbf{l} \cdot \mathbf{h})^5$
把fresnel项带入,就得到
$\int_{\Omega} \rho(\mathbf{l},\mathbf{v}) (\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
$=\mathbf{c}_{spec}\int_{\Omega}\frac{\rho(\mathbf{l}, \mathbf{v})}{F(\mathbf{v},\mathbf{h})}(1-(1-\mathbf{v} \cdot \mathbf{h})^5)(\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
$+\int_{\Omega}\frac{\rho(\mathbf{l}, \mathbf{v})}{F(\mathbf{v},\mathbf{h})}(1-\mathbf{v} \cdot \mathbf{h})^5(\mathbf{n} \cdot \mathbf{l}) d \omega_{i}$
方程右边的两个积分项可以分别预计算成一个LUT的两个通道,查找参数是roughness和cos(theta),LUT的输出又很好地能落在[0, 1]之间。
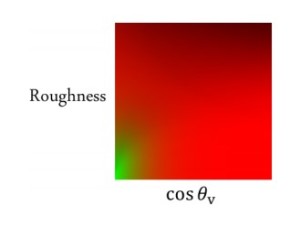 使用的时候,只需要用roughness和cos(theta)读取这个LUT,这样就能计算出specular的IBL结果:prefiltered-cubemap * (specular * LUT.x + LUT.y),得到的结果和ground truth很接近。由于有了这个LUT,不再需要计算BRDF,只要一次乘加。Prefiltered cubemap只要采样一次,在NVS 4200M上也可以轻松达到110FPS,完全到了实用的范围。
使用的时候,只需要用roughness和cos(theta)读取这个LUT,这样就能计算出specular的IBL结果:prefiltered-cubemap * (specular * LUT.x + LUT.y),得到的结果和ground truth很接近。由于有了这个LUT,不再需要计算BRDF,只要一次乘加。Prefiltered cubemap只要采样一次,在NVS 4200M上也可以轻松达到110FPS,完全到了实用的范围。
本篇重现了UE4的环境BRDF,用的是GGX的BRDF。下一篇会试着换用KlayGE的blinn-phong BRDF。






Comments